| Fourier (baron Joseph - Auxerre 1768 - Paris 1830) est un mathématicien, physicien, politicien français. Il est étudiant à l'école normale de l'an III, devient membre du corps enseignant de l'école polytechnique en 1795. L'étude de la propagation de la chaleur l'a amené à la découverte des séries trigonométriques portant son nom. Il devient membre de l'académie des sciences en 1817, puis secrétaire perpétuel en 1822. Il entre à l'Académie française en 1826. |

|

a0 est le coefficient et (a1cos x + b1 sin x) par exemple un des termes de notre somme.
Il suffit maintenant de déterminer les coefficients a0, an, et bn, pour cela on utilise les formules suivantes :
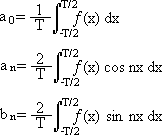
Quelques exemples concrets parleront certainement mieux, en voici deux, rencontrés souvent en électronique, puisqu'ils font partie des signaux disponibles en sortie des générateurs de fréquences. Je passe volontiers sur les démonstrations, cet article se veut le plus généraliste possible, les plus mathématiciens d'entre vous pourrons se reporter aux nombreux articles disponibles sur internet, de plus l'objet de cet article est de montrer comment calculer une transformée de Fourier par échantillonnage, donc par calcul informatique, sans utiliser de démonstrations.
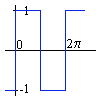
il se décompose de la manière suivante :
f(x) = 4/Pi (sin x + sin 3x / 3 + sin 5x / 5 + sin 7x / 7 + ... sin nx / n + ...), avec n toujours impair.
Deux remarques, d'une part nous n'avons que des termes en sinus, et d' autre part les coefficients sont impairs.
Si vous disposer d'une calculatrice graphique ou un logiciel permettant de tracer des courbes, vous pouvez vérifier la ressemblance avec quelques termes. le mot marqué Pi (le langage HTML qui est utilisé pour l'écriture et la présentation de cette page n'est pas conçu pour la représentation de symboles mathématique) est le fameux nombre qui commence ainsi : 3,1415926.
Sur une calculatrice fx .... graphique (je ne citerais pas la marque ...), il faudra d'abord passer en mode radian, puis entrer la formule :
en prenant pour échelle en Xmin = -4, Xmax = 4, Ymin = -1.2 Ymax = 1.2
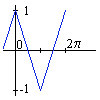
le résultat est f(x) = Pi/4 (cos x + cos 3x / 9 + cos 5x / 25 + cos 7x / 49 + ... cos nx / (n x n) + ...), avec n toujours impair.
Remarque quasiment identique à la précédente : que des termes en cosinus, et un coefficient impair.
Sur la calculatrice toujours en radian et en conservant l'échelle cela donne :
La courbe obtenue est au passage beaucoup plus proche d'un triangle que n'est proche du carré la courbe précédente.
Avant de passer à l'analyse d'un signal audio, il faut tout d' abord voir, ou revoir quelques notions concernant les sons.
Un son physiquement possède les quatre caractéristiques qui sont les suivantes :
|
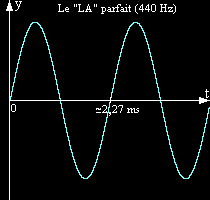
La fréquence : prenons par exemple le diapason, car d'une part cet "instrument" ne joue qu'une note le LA, et d'autre part c'est celui dont la vibration approche le plus la sinusoïde parfaite (f(x) = sin x). Le LA du diapason est défini au niveau international comme ayant une fréquence de 440 Hz (Hertz), c'est le nombre de vibrations produites à chaque seconde, cette caractéristique du son s'appelle la fréquence, cela veut aussi dire que tous les 1/880 de seconde (environ 1,14 ms) on a une nouvelle période (au bout d'environ 2,27 soit 1/440 on est à la fin de la seconde période). Au passage plus la fréquence est élevée et plus le son est aigu, et d'autre part un doublement de la fréquence se traduit par un changement d'octave, c'est à dire que la fréquence 880 Hz correspondant au LA de l'octave suivant. L'oreille humaine décèle des sons compris entre 16 et 20000 Hz. Pour information les fréquences des instruments de musique et de la voix sont comprises grosso modo entre 50 et 4 000 Hz. |
|
| Pour écouter le LA cliquez sur les notes de musique suivante. |
- La tonalité d'invitation à numéroter est une onde continue à 440 Hz.
- La tonalité d'acheminement (n'existe plus) était une onde de 440 Hz d'une durée de 50 ms, suivie d'un silence de 50 ms.
- La tonalité d'occupation est une onde de 440 Hz d'une durée de 500 ms, suivie d'un silence de 500 ms.
- La tonalité de retour d'appel est une onde de 440 Hz d'une durée de 2 secondes, suivie d'un silence de 3 secondes.
L'amplitude : un son se distingue aussi par une autre propriété qui est son amplitude. Si vous jouez du piano avec la sourdine afin de ne pas gêner les voisins l'amplitude est moins importante. L'amplitude représente la puissance du son. Cette caractéristique se mesure en dB (Décibel), à un accroissement de 3 dB correspond à peu de choses près à un doublement de la puissance sonore. L'amplitude sur la courbe précédente est représentée par les valeurs sur l'axe des y.
Le timbre : les instruments autres que le diapason ou bien la voix quand on tente de chanter une note "juste" n'ont pourtant pas la même sonorité, c'est parce qu'ils jouent d'une part la fréquence demandée (appelée fondamentale), et en plus de cela génèrent d'autres fréquences appelées harmoniques (double, triple, quadruple, ... de la fondamentale (la fondamentale est la fréquence de base), cette caractéristique s'appelle le timbre. Le timbre est aussi modifié par le milieu qui véhicule le son, un son sera différent s'il est véhiculé par l'air, l'eau, d'autres matériaux comme le bois, certaines fréquences sont en effet absorbées par le milieu véhiculant le son. Enfin, la dernière caractéristique d'un son est sa durée, ce point ne mérite pas d'explications particulières.
L'ensemble de la fondamentale et des harmoniques forme ce que l'on appelle le spectre du son. Le spectre du son est aussi formé de bruits et de transitoires.
Pour cela il faut tout d'abord échantillonner le son, c'est à dire que l'on demande par exemple à la carte son de récupérer à un moment donné une certaine portion du son à une vitesse d'échantillonnage fixée, dans le cas de CD-PRO la vitesse d'échantillonnage est fixée à 18 000 Hz,là vous allez peut être faire une faire une remarque, un son nous l'avons vu est audible entre 16 et 20 000 Hz, alors pourquoi les cartes son échantillonnent elles jusqu'à 44 100 Hz, 48 000 Hz pour certaines, et pourquoi les CD audio sont ils gravés à 44 100 Hz ? En fait il faut toujours échantillonner à une fréquence double de la plus haute fréquence susceptible de se produire, c'est pour cela qu'un CD malgré qu'il soit gravé avec un son numérisé à 44 100 Hz ne sera capable que de rendre fidèlement des sons que jusqu'à 22 050 Hz, pour ceux que cela intéresse c'est SHANNON (Claude Elwood né en 1916 à Gaylord, Michigan) un mathématicien américain qui a démontré qu'il fallait échantillonner au double de la fréquence maxi recherchée, qui est connu comme le théorème de SHANNON (SHANNON est avec Warren WEAVER à l'origine de la théorie de l'information). CD-PRO pour sa part ne peut analyser que des sons jusqu'à 11 025 Hz, ce qui est amplement suffisant compte tenu que les sons habituellement audibles vont jusqu'à 4 000 Hz comme vu précédemment, seules quelques harmoniques par moment se font pressentir dans la partie droite de l'analyseur de spectre, et encore rarement.
Passons maintenant à l'analyse, nous avons recueilli quelques octets, ces octets prennent des valeurs d'amplitude comprises entre 0 et 255, (CD-PRO échantillonne sur 8 bits, ce qui est largement suffisant par rapport au résultat à rechercher), mais le point milieu de l'octet est la valeur 128 en dessous ce sont les valeurs négatives et au dessus ce sont les valeurs positives, en fait cela revient à considérer qu'un octet contient une valeur entre -128 et 127 (ce sont des octets signés par exemple en langage C ils sont appelés signed char). Il faut considérer des valeurs négatives comme positives car nous avons vu dans nos exemples précédents (avec les signaux carrés et triangulaires) que le signal sonore traverse l'axe des abscisses.
Cela étant fait, nous considérons cet échantillon comme notre intervalle de temps comme c'était le cas entre 0 et 2Pi dans les exemples précédents, on considère le premier octet échantillonné comme le point 0, et le dernier comme le point 2Pi, les octets compris dans l'intervalle ayant une valeur angulaire x au prorata de l'intervalle [0, 2Pi[. Notre échantillon d'une certaine longueur a donc une durée, qui correspond donc à notre fréquence fondamentale. Prenons un petit exemple, on échantillonne par la carte son, et on récupère 1000 points de mesure, supposons que notre ensemble représente une sinusoïde complète, cette dernière aura donc une fréquence de 18 000 / 1 000 soit 18 Hz (la fréquence d'échantillonnage divisée par les 1 000 points de mesure). Dans le même intervalle pourrait se trouver deux sinusoïdes de fréquence 36 Hz et ainsi de suite.
On calcule cette fréquence fondamentale et toutes les harmoniques que CD-PRO a besoin de calculer, soit 49 fréquences dans ce cas particulier. CD-PRO est écrit en assembleur pour que le calcul s'effectue rapidement, de plus l'algorithme est optimisé pour simplifier au plus les calculs.
Au niveau du calcul on va utiliser les formules nous permettant de calculer a0, an et bn. Ensuite il nous reste à récupérer pour chaque valeur de x, sa valeur f(x), soit y, soit l'amplitude correspondante.
// Déclaration des variables et constantes.
const harmo=48 // Si on prend 48 harmoniques.
const maxech=1000 // Si on prend 1000 échantillons.
entier i
entier h
réel buffer [ech] // buffer destiné à contenir les échantillons.
réel a0 // variable contenant la fondamentale.
réel an [maxech] // buffer contenant le résultat de an cos x.
réel bn [maxech] // buffer contenant le résultat de bn cox x.
réel en [maxech] // on l'utilisera par la suite.
// On par du principe que a0 est nulle ainsi que toutes les valeurs de an [h], et bn [h].
// calcul de la fondamentale. début
-
pour i variant de 1 à maxech
faire
-
a0 = a0 + buffer [i];
a0 = a0 / maxech; // cela revient en fait à calculer la valeur moyenne de l'amplitude des échantillons.
// Calcul des harmoniques
pour h variant de 1 à 48 // La version 2 de CD-PRO calcule 48 harmoniques.
faire
- pour i variant de 1 à maxech
faire
- an [i] = an [i] +
(buffer [i] * cos (h * (ech / (maxech * 2 * Pi))
bn [i] = bn [i] + (buffer [i] * sin (h * (ech / (maxech * 2 * Pi))
an [h] = 2 * an [i] / ech
bn [h] = 2 * bn [i] / ech
En fait cela n'est pas tout à fait fini, on obtient en général pour chaque fréquence une valeur pour an et une valeur pour bn, et on aimerait traduire des deux valeurs en une seule qui serait affichable sous la forme d'une barre unique, pour cela on utilise la formule de PARSEVAL, on a pour chaque fréquence l'énergie en = an x an + bn x bn (cela nous permet de plus d'obtenir des valeurs positives)
on termine donc avec les lignes de code suivante :
-
a0 = a0 *
a0
pour h variant de 1 à 48
faire
-
en [h] = an [h] *
an [h] + bn [h] *
bn [h]
et c'est terminé et cela fonctionne très bien ...
Les transformées de Fourier et leurs inverses sont très utilisées en informatique dans le traitement du signal, avec pour exemple les traitements de signaux sonores, de mesures de tensions et d'intensités en tous genres, en imagerie (compression d'images voir amélioration d'images floues (si le défaut ayant provoqué le flou est connu). Il existe du reste des processeurs spécialisés dans le traitement numérique du signal, ils sont appelés DSP (Digital Signal Processor), la transformée de Fourier fait en général partie de leurs panoplies.